オフィス近くの寺院の今月の標語は「楽を求めて苦しむ」。こういうことばに反応して「じゃあ、苦を求めたら楽になるんだなあ」と推し量るのは単純な早とちりというものだ。《命題の逆・裏・対偶》。聞いたことがある、ちょっとかじったことがあるという程度の人が大勢いるはず。覚えたつもりが、しばらく経つとすっかり忘れてしまう論理ツール。論理的思考は研修テーマの一つなのでぼくには染みついているが、いざこれを説明して理解してもらうとなると話は簡単ではない。
楽を求めるから苦しむ、ならば、その逆の「苦を求めれば楽になる」が真理だと考えてしまうのが人の常だろうが、Xがダメなら、その真逆のYはいいはず……と導出するのは甘い判断と言わざるをえない。ふだん理屈を嫌う人ほどこんなふうに二律背反的に物事を発想する傾向がある。山で右の道が行き止まりだったとして、元の位置から左へ行けば正解かと言うと、そうとはかぎらない。どちらも行き止まりの場合だってあるのだ。
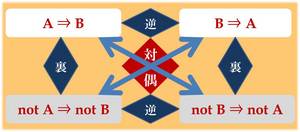
「楽を求めて苦しむ」をわかりやすく「楽⇒苦」と表現してみよう。図では〈A⇒B〉という命題の位置に入る。これを論理学の「逆」に置換したのが〈B⇒A〉で、「苦⇒楽」に相当する。つまり、「苦しみを求めて楽になる」。さらに、論理学には「裏」という概念もある。〈not A⇒not B〉がそれ。「楽を求めなければ苦しまない」という命題表現になる。たいせつなことは、〈A⇒B〉が真理だとしても、順序をひっくり返した〈B⇒A〉と、否定形で裏返した〈not A⇒not B〉が真理とはかぎらない、という点である。
命題が真理だとしても、逆と裏は真理かもしれないしそうでないかもしれないということは、ちょっと考えてみればわかる。「ふだんから楽なことばかりしたり求めたりしていては、困難な場面に出くわすと対応できなくなって苦しんでしまう」……これに納得したとしよう。では、逆の「ふだん敢えて苦しいことを求めて実践していたら、いざという場面で楽になるか」と言えば、そうとはかぎらないことに気づく。そう、いつも苦しいかもしれないのだ。さらに、裏の「楽なことを安易に求めようとしなければ、苦しむこともないだろう」にも賛成しかねる。もしかすると、苦しみはいつもついてまわるのかもしれないではないか。
この論理図式の中央に「対偶」というのがある。〈A⇒B〉が真理ならば〈not B⇒not A〉がつねに真理になるというロジックだ。つまり、「楽を求めて苦しむ」のが真理なら、「苦しんでいないときは楽を求めていないときである」が必然導かれるのである。命題の対偶について心得ておくことは、ものを考えるうえでかなり便利だと言えるだろう。と、これを結論としてここで終えるわけにはいかない。
これはあくまでも論理図式の「もし～が真理ならば」という前提に立ったときの話にほかならない。すでにぼくたちが知っている命題、たとえば「東京は日本の首都である」なら、その対偶である「日本の首都でないならば東京ではない」は確定する。だが、現実は命題そのものの真偽が定まらないことが圧倒的に多いのだ。逆や裏や対偶云々の前に、命題そのものを問う力こそが求められるのである。
